Teaching the Toaster to Feel Love [Part 1]

Every so often you find yourself confronted with a problem that you as a human can answer, but to express it algorithmically in code would be very difficult. In these times people often turn to machine learning to solve their problem. However, machine learning is a enormous field and it’s difficult finding where to even begin.
As new devices are developed to interface with humans for games and other applications; accelerometers, gyroscopes, depth cameras with skeletal tracking and who knows what next. Interpreting the input reliably has become a much more difficult task.
So I wanted to write a series of posts which hopefully will benefit anyone wanting to learn how to use one variety of machine learning; Support Vector Machines (SVM).
Introduction
An SVM makes a binary decision about a feature vector deciding if it is closer to the positive class or the negative class. During the training process for an SVM it’s given many feature vectors that exist as examples of what kinds of data appears in the positive vs. negative classifications.
Here is a breakdown of a class,
Class
{
Feature Vector 1 { Feature 1, Feature 2, … },
Feature Vector 2 { Feature 1, Feature 2, … },
…
}
So what is a feature? A feature is simply a floating point number that has some special meaning as far as the programmer is concerned. To the SVM however, it’s just a number in a dimension. So as you can see the inputs for a class are nothing more than a list of vectors filled with floats.
To determine the best best hyperplanes (support vectors) that best divide the data you have to train the SVM with example feature vectors for each class. The trick is finding the support vectors that maximize the margin (distance) on either side of the hyperplane. The easier it is to split the data, the less likely you are to see incorrectly classified data when you put the system to use.
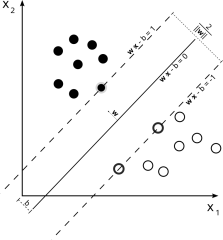
So let’s talk examples, if I were to say the following feature vector { 0.25 } was the only feature vector in the positive class, and feature vector { 0.75 } was the only feature vector in the negative class, the ideal support vector would be { 0.50 } because it best divides the data, giving the greatest margin between both classification feature vectors. Which is easy to see when you have only 1 feature and 1 feature vector in either class. The problem becomes infinitely more difficult when you have classes of 10,000 feature vectors with 600 features in them each being used for training data.
There are several kernel types used to find the best hyperplane through the features. Linear, Radial Basis Function (RBF), Sigmoid, and Polynomial. From the papers I’ve read, RBF seems to be quite popular.
Next Time
For the first post I just wanted to introduce the basic vocabulary. Next time I’ll get into actually using them in practice.
